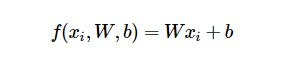Thanks to Tony Stark and Elon Musk, everyone seems to be talking about the AI, Big Data and Machine Learning, even though very few actually understand them thoroughly. To most people AI is a magical tool fuelling Self-Driving Cars, Robots and the ever ubiquitous recommender systems among other magical things. True indeed, most Machine Learning (ML) models are black boxes, trained by copious quantities of data. They are fed with data from which they learn but little is known on they learn and what each unit will learn. .
 |
| Definitely magic |
But its not ..
Backed by calculus and linear algebra, Machine Learning is far from magic. Having learnt how the models learn I was curios to interpret what the models actually learnt.
Support Vector Machine (SVM)
This is no doubt one of the simplest models used for classification. Given input data with dimensionality D, C different classes of output and X outputs, it uses a score function to compute scores for different classes and assigns the input to the class with the highest score.
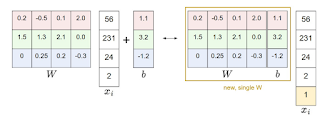
where W is C*D weight matrix, xi is D*1 input sample vector, and b is C*1 bias vector. The result is a C*1 score vector with a score for each of the C classes; the output will be the class with the highest score. This operation can be visually represented as follows:
Each row i of W can be interpreted the ideal vector for a corresponding class and the product Wxi as a cross product that measures the similarity between the respective class and the input. The closer they match, the higher the score and vice versa. For Image Classification, proving this is as easy as plotting each row of W of a trained model, as a D-dimensional image.
Taken from the Stanford course cs231n website, these images reveal what the model what each class should look like. The uncanny similarity between a deer and a bird speaks volumes about the small capabilities of the SVM. Although they are easily trained and interpreted, they don't exactly produce the best results, hence the need for more sophisticated models; Neural Networks.
Neural Networks.
Built from SVMs, Neural Networks (NN) are made of SVM-like units called neurons, arranged in one or more layers. Unlike SVMs , neurons have one output computed with a sigmoid like activation function which indicates whether a neurons fires or not. it is due to this complication that Neural Networks are universal approximators, capable of approximating every function, of course at the expense of transparency.
Folks at Google accepted the challenge and published interesting results in their famous inceptionism. By turning the network upside down, they were able to show what the network learnt about each class. For instance, in the image below, this is what the network learnt about bananas from random noise.
In addition, they also deduced that the higher up the layer is, the more abstract features it detects. That is , . This was done by "asking" a network layer to enhance what it learnt from the images. Lower layers detected low-level features and patterns like edges and strokes.
 |
| Patterns seen by low layers |
Higher layers produced more interesting images, things you'd see in your dreams.
Even more interesting are Recurrent Neural Networks (RNN's), Neural Networks with memory that are used predicting sequences. In his famous blogpost, Andrej Karpathy (a Deep Learning researcher should know ), wrote not only on how effective they are but also how they can be interpreted. Using LSTM variant, he was able to generate interesting texts like Paul Graham's essays, Shakespeare's poems, research papers all the way to the Linux database.. In addition to that, he was able to single out what some neurons detected. Only 5% of the neurons detected clearly defined patterns but these patterns are interesting to say the least.
 |
| This one fired on lines end |
| This one fired on texts between quotes. |
NB:Red indicates higher activation compared to blue.
I hope this is enough to convince you that AI isn't black box magic that computers will use to exterminate mankind, but a very scientific process. It may not be clear what each neuron will learn, but we can control what it will learn using hyper parameters and regularization. and after training, figure out what each has learnt.
No doubt, the original neural network, the brain does something learns in a similar way. Just as how connection weights are strengthened through back propagation, neurons enforce connections that are repeatedly used. Neuroscientists refute this claim but what is true in both cases is that learning is highly influenced by input data and hypermaterers. In NNs these hyperparameters includes the learning rates and regularization constants while in the brain these hyper parameters are influenced by emotions, curiosity, and frequency of learning. We can't control all of them but we can definitely control the kind of data we feed our brains, and how often we do so. On that note, what stuff are you feeding your brain, What fires your neurons? Have a great week ahead!